# 이전 강의 복습
sigmoid는 vanishing gradient라는 문제점이 있었다.
ReLU를 대부분 선택하는데, 잘 작동하기 때문이다.

weight 초기화
초기 weight가 너무 작으면 activation이 0으로 되고 gradient도 0가 되고 학습이 진행되지 않는다.
초기 weight가 너무 크면 activation이 saturate(뭐라고 해석해야하지)되고 gradient도 0이 되고 학습이 진행되지 않는다.
초기 weight를 적당하게 하려면 Xavier나 MSRA 초기화를 활용할 수 있다.

Data preprocessing
normalization(정규화 -> 데이터를 0에서 1 사이로)를 해준다.
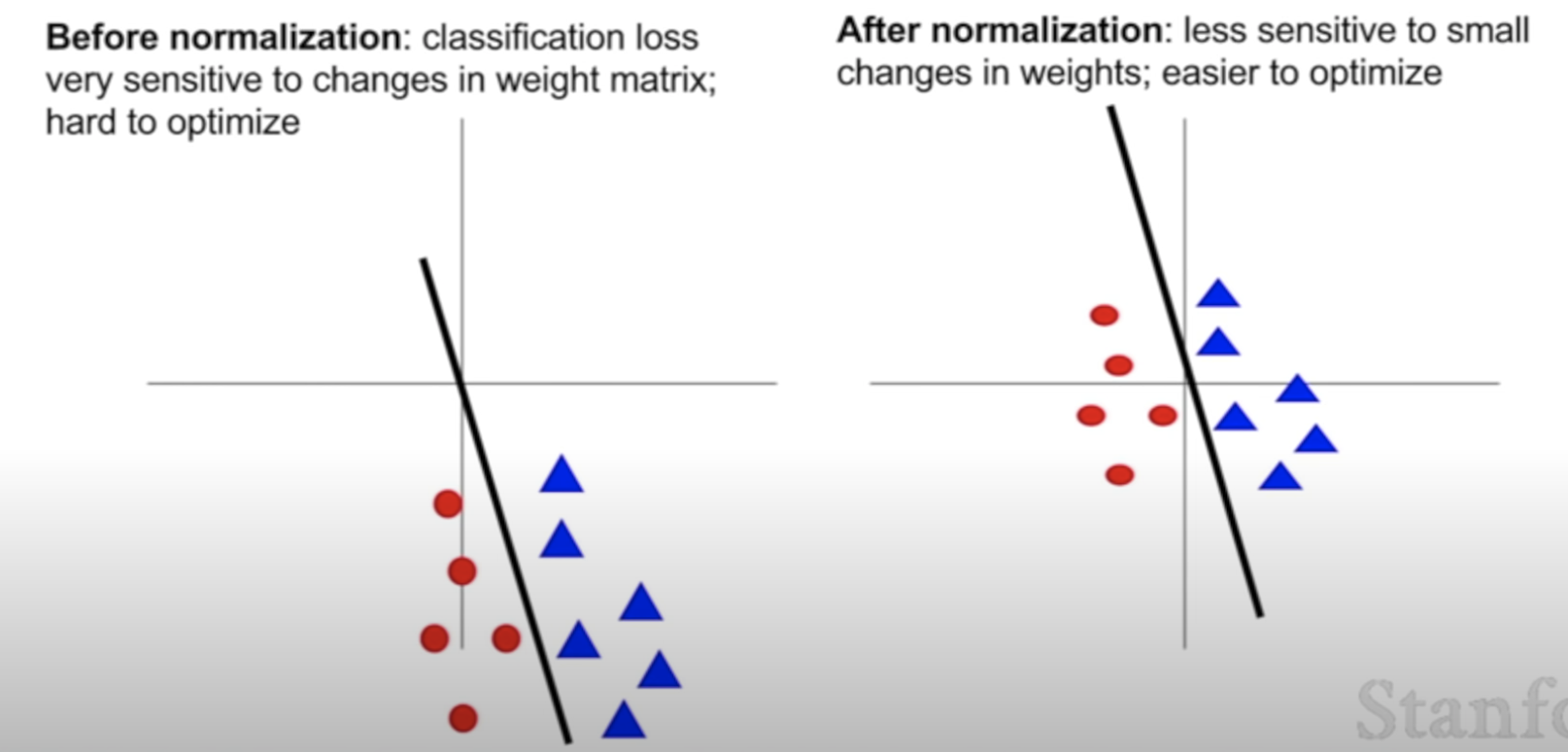
정규화를 하지 않으면 loss가 가중치의 변화에 너무 민감하게 반응한다.
반면, 정규화를 해주면 데이터가 0에서 1 사이로 정규화되기 때문에 가중치에 덜 민감하게 loss가 반응하게 되어 학습에 용이하다.
Batch Normalization
중간의 activation들의 평균이 0이 되고, 분산이 1이다.

이거 해석...좀....
Babysitting Learning
Learning Rate에 따라서 달라지는 1) loss 그래프,
training set에 과적합되어 있어 보이는 3) Accuracy 그래프 -> Regularization(weight에 패널티 부여)이 필요해 보인다.

하이퍼파라미터 찾기
1) Grid Layout
2) Random Layout -> 이론적으로 이게 더 나음

# 오늘 배울 내용
- optimization
- Regularization
- Transfer Learning
# Optimization
그림의 x축은 가중치1, y축은 가중치2이다.
loss function을 가장 줄여주는 빨간색 부분을 찾아가는 것이 optimization이다.
아래 코드는 SGD를 표현한 것이다.
gradient를 loss function, data, weight를 가지고 판정한 다음, step size(=Learning Rate)와 곱하여
기존의 weight에서 빼준다. (loss이기 때문에)

SGD의 문제점
- 만약, loss 변화가 한 방향에서만 빠르고 나머지에서는 느리다면? gradient descent는 어떻게 될 것인가?
얕은 차원에서는 매우 느리고, 가파른 차원에서는 ??

- local minima or saddle point 문제
: 중간에 멈춰버린다.
* 고차원 문제로 가면 saddle point가 거의 대부분의 지점에서 일어나므로 사실상 의미가 없다.

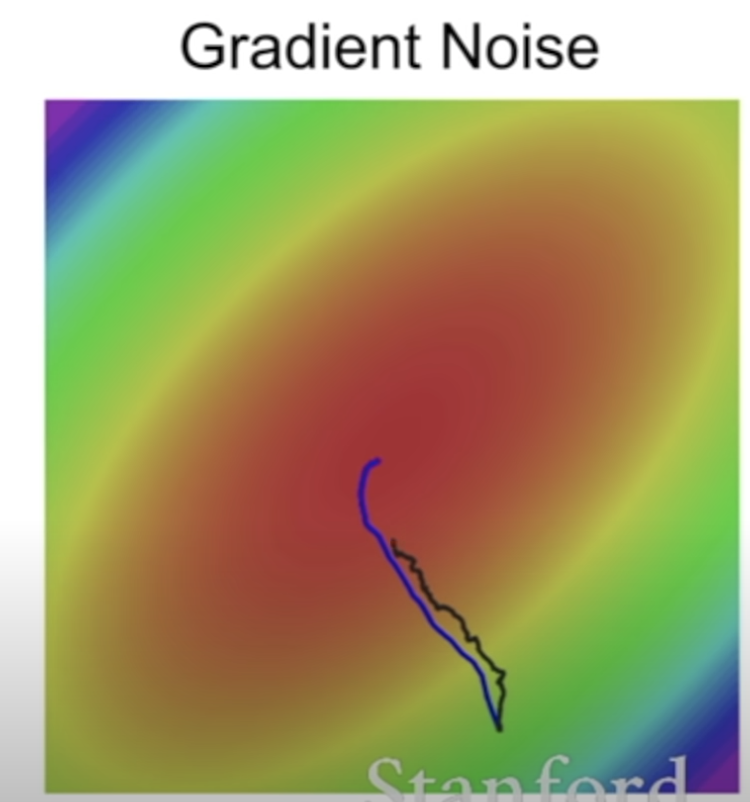
- 모든 데이터를 사용하는 것이 아니라, 미니 배치로 일부를 가지고 하는 것이기 때문에 진짜 정보를 활용하지 못한다. 노이즈를 갖게 된다.
# 해결책 : Momentum

* rho는 일반적으로 0.9나 0.99이다.
velocity(vx)를 gradient의 평균으로서 계속해서 빌드업한다. <- 핵심
velocity에는 이전 gradient들이 축적되어 있으므로 gradient가 매우 작은 부분이더라도 velocity가 있으므로 멈추지 않는다.
1) local minima나 saddle point에서 멈추지 않고 계속해서 나아갈 수 있는 힘이 생긴다.

2) 또한, gradient 추정치가 평균되어 노이즈가 적어지는 장점이 있다.
# Nesterov Momentum
*convex optimization에서는 좋은 이론적 특징을 가지고 있지만, non-convex 문제에서는 쓸모가 없어진다.

# Adagrad

* 계속해서 학습이 진행되면?
grad_sqaured가 엄청 켜져서 x 는 거의 사라진다.
# RMSProp
Adagrad 문제를 좀 더 늦춘다.


SGD+Momentum보다 RMSProp이 더 느리지만, 정확하게 간다. SGD+Momentum은 도착해서 휘어지는것을 볼 수 있다.
# Adam(제일 많이 씀)
Momentum + RMSProp


Adam이 좀 더 휜다.
# decay Learning rate
처음에는 decay 없이 하고, decay 어떻게 넣을지 보기


# BFGS
- First-order optimization

- Second-order optimization


-> Learning rate가 없다는 장점있다.
하지만, non-convex 문제에서는 잘 작동하지 않으므로, 잘 쓰지 않는다.
So, Adam을 디폴트로 쓰고, 풀배치로 돌릴 수 있다면 L-BFGS를 사용할 것.
# 추가적인 tips
- ensemble
- regularization : Dropout, Batch normalization, Data augmentation, fraction max pooling
# Dropout
랜덤하게 뉴런을 0으로 지정하여 삭제한다. -> 피쳐들간의 co-adaptation을 막아준다. overfitting 막아준다.
fully connected layer나 convolutional layer에서 많이 사용한다.

Dropout : Test time -> 결과가 일관되지 않으므로 성능이 좋지 않음.
# General Dropout

# Trick -> Inverted dropout
GPU가 좀 더 쉽게 학습할 수 있게 하도록.

* batch normalization도 비슷한 작용을 하기 때문에 Dropout과 Batch normalization을 동시에 사용할 필요가 없을 때가 있다.
하지만, Dropout은 batch normalization와 다르게 p값으로 normalization 정도를 조정할 수 있다는 장점이 있다.
# Data Augmentation
데이터를 다양하게 시도해볼 수있도록 해준다. train/test에 모두 해줄 수 있다.
# Fractional max pooling
랜덤으로 맥스 풀링 적용
# Transfer Learning



'AI > CS231n' 카테고리의 다른 글
| [Lecture 10] Recurrent Neural Networks (0) | 2022.07.06 |
|---|---|
| [Lecture 8] Deep Learning Software (0) | 2022.07.05 |
| [Lecture 6] Training Neural Networks I (0) | 2022.05.18 |
| [Lecture 5] Convolutional Neural Networks (0) | 2022.05.17 |
| [Lecture 4] Introduction to Neural Networks (0) | 2022.05.17 |