1. 가설검정의 순서
1) 가설의 설정
2) 검정통계량의 선정
3) 유의수준의 결정
4) 검정규칙의 설정
5) 자료수집 및 검정통계량 계산
6) 가설의 채택/기각 결정
2. 가설의 설정
- 귀무가설(Ho) : 기존의 알려진 지식이나 이론, 입증할 필요가 없는 가설
- 대립가설(Ha) : 주장하고자 하는 지식이나 이론, 입증할 필요가 있는 가설
[예] 기존의 알려진 과학 이론이 있는데, 어느 학자가 새로운 이론을 주장한다면
Ho : 기존의 과학 이론이 옳다.
Ha : 새로운 이론이 옳다.
3. 귀무가설과 대립가설의 유형
1) 양측 검정
Ho : θ = θo
Ha : θ ≠ θo
< 단측 검정 >
2) 우측 검정
Ho : θ <= θo
Ha : θ > θo
3) 좌측 검정
Ho : θ >= θo
Ha : θ < θo
** 귀무가설이나 대립가설은 채택할 수는 없고, 기각하지 못 한다라고 표현하는 것이 원칙이다.
4. 유의수준 결정
유의수준 : 일어날 가능성이 희박하다고 생각되는 확률 수준으로 귀무가설을 기각하는 기준이 된다.
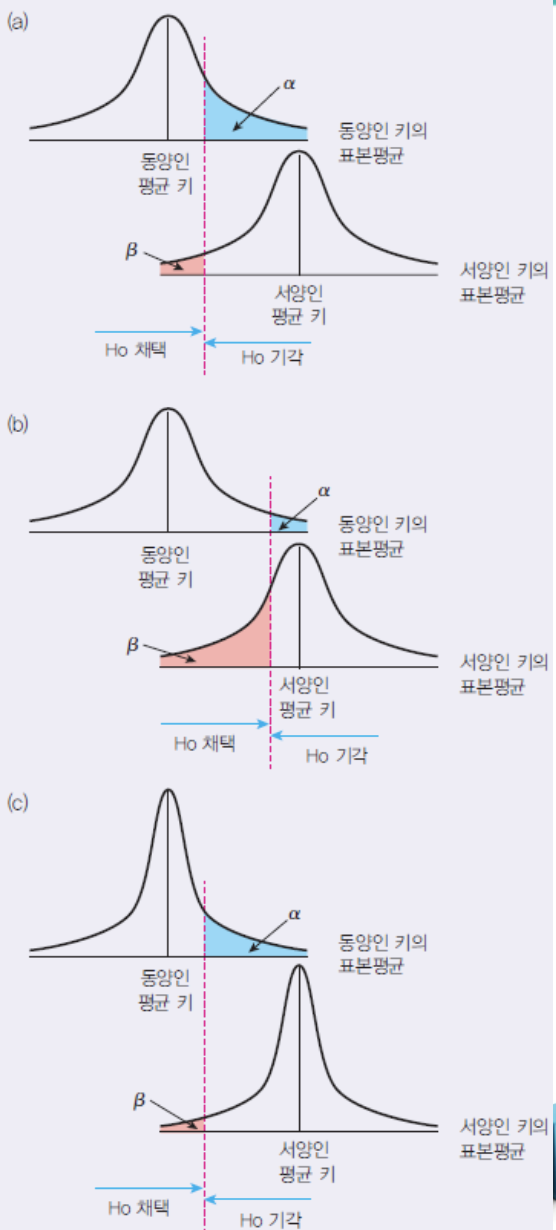
제 1종의 오류 : Ho가 사실임에도 불구하고, 이를 기각하는 오류
제 2종의 오류 : Ho이 허위임에도 불구하고, 이를 채택하는 오류

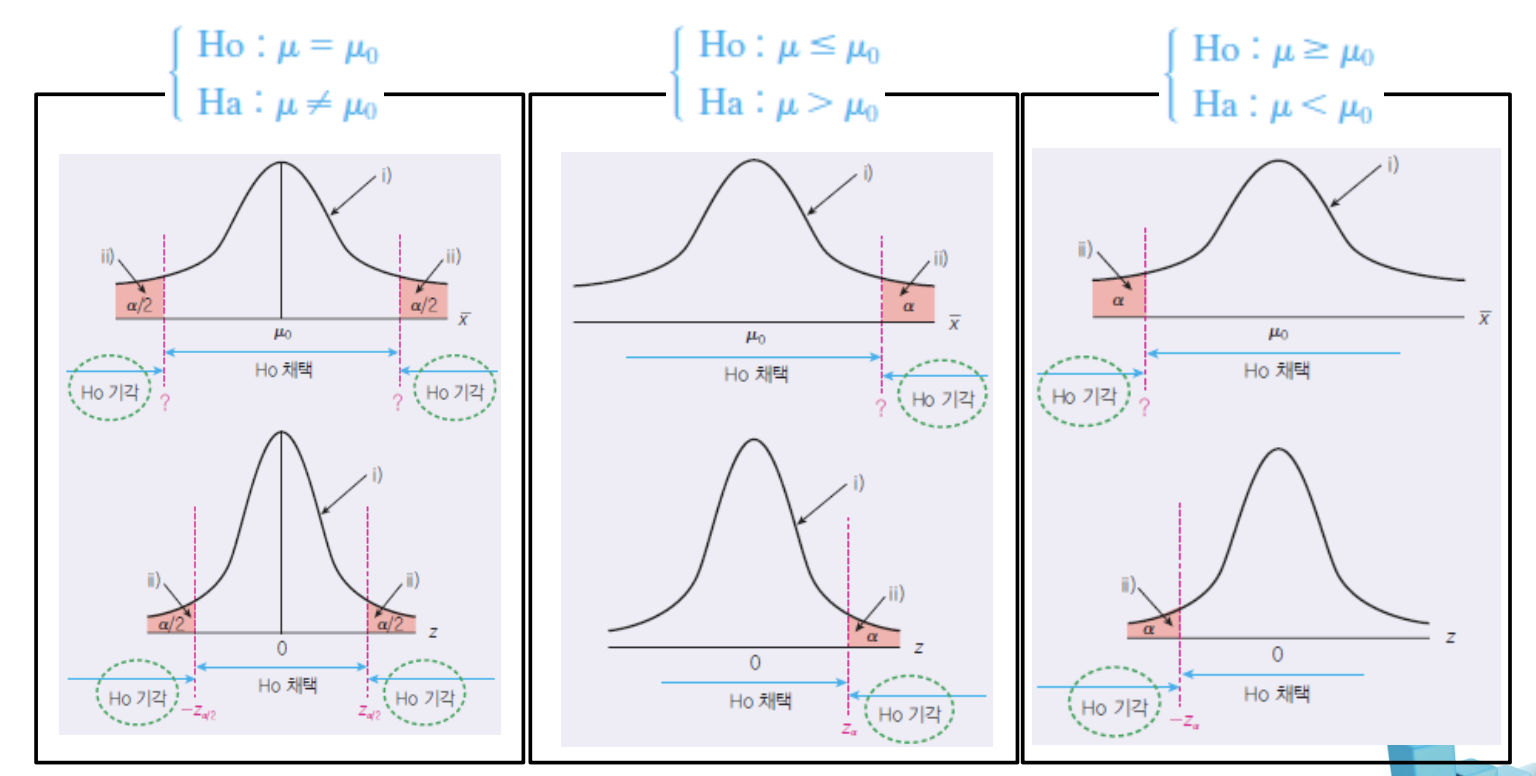
5. 검정규칙의 결정
6. 자료수집 및 검정통계량 계산
: Z분포 또는 t분포 식을 이용한다.
7. p-값이란?
: 귀무가설이 사실이라는 가정 하에서 관측된 결과보다 극단적인 결과가 발생할 확률이다.
< p-값 vs 알파 값 >
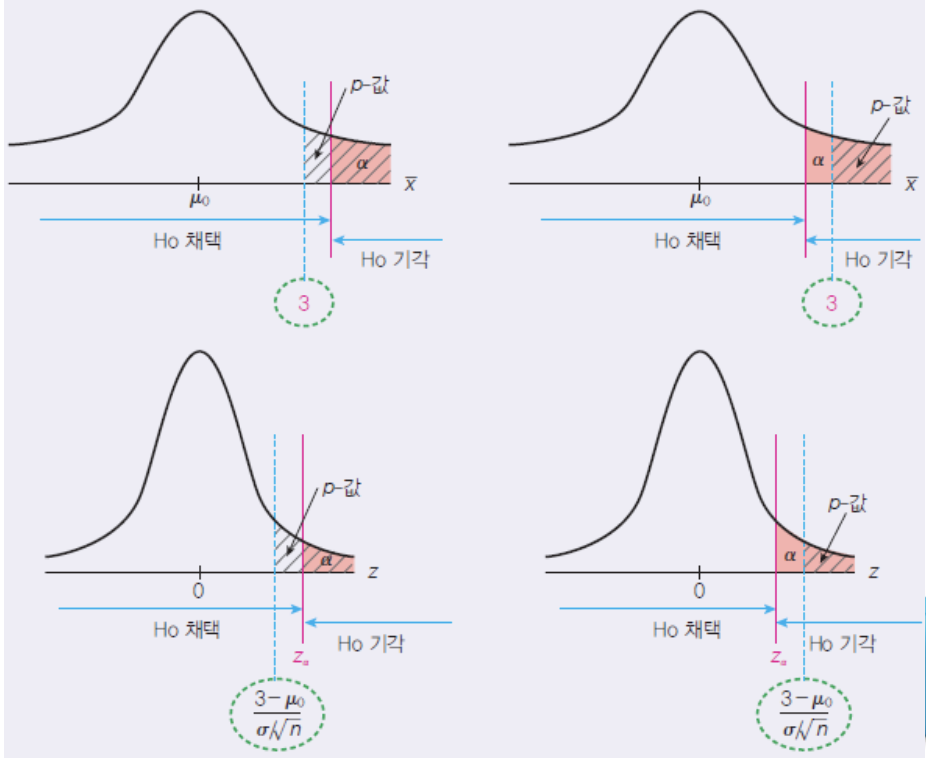
-> p-값 >= α 이면 귀무가설을 채택한다.
-> p-값 < α 이면 귀무가설을 기각한다.
8. 모비율 / 모분산 / 모평균에 대한 가설검정
1) 모비율의 검정통계량의 산정
Z = P^ - p0 / √(p0(1-p0)/n) ~ N(0, 1)
2) 모분산의 검정통계량의 산정
V = (n-1)S^2 / σ ~ X^2(n-1)
3) 모평균의 검정통계량 산정
Z = X바 - μ / (σ / √n)~N(0,1)
또는
T = X바 - μ / (S / √n)~t(n-1)
'AI > Statistics' 카테고리의 다른 글
| 4. 두 모집단 비교에 대한 추정과 검정 (0) | 2020.12.14 |
|---|---|
| 2. 추정 : 모집단이 하나인 경우 (0) | 2020.12.12 |
| 1. 모수와 통계량의 관계 : 표본 분포 (0) | 2020.12.12 |