가전제품 이것저것 이야기

1. 추정의 개념

1) 점추정 : 한 수치로 추정

2) 구간추정 : 구간으로 추정

ex) 직장인의 평균 근무시간에 대한 추정

점추정 : 8.5시간

구간추정 : 7.8시간부터 9.2시간 사이

2. 점추정

추정량 : 공식

추정값 : 공식에 따라 계산된 수치

표본추출오차의 크기 : E[(θ^ - θ)^2] = E[(θ^ - θ)^2]+Var(θ^)

(θ^ : 추정량, θ:모수)

-> 표본추출오차가 작으려면 위의 값들이 작아야 한다.

- 좋은 추정량의 요건 

: 불편성(E(θ^) = θ),효율성(분산이 제일 작은 추정량),일치성

3. 불편성

추정량이 E(θ^) = θ 의 조건을 만족할 때, 이 추정량은 불편성을 만족한다고 한다.

이때, θ^를 모수 θ의 '불편추정량'이라고 부른다.

-> E(X바) = μ, E(S^2) = σ^2,E(P^)=P이므로

추정량 X바, S^2, P^은 각각 모평균, 모분산, 모비율의 불편추정량이다.

불편추정량(대포1) vs 편의추정량(대포2)

-> 표본평균은 불편추정량이나, 중앙값은 편의추정량이다.

4. 효율성

: 불편추정량 중에서 분산이 작은 추정량을 효율적이라고 한다.

-> 셋 중에서 (1)이 효율성을 만족한다고 볼 수 있다.

5. 일치성

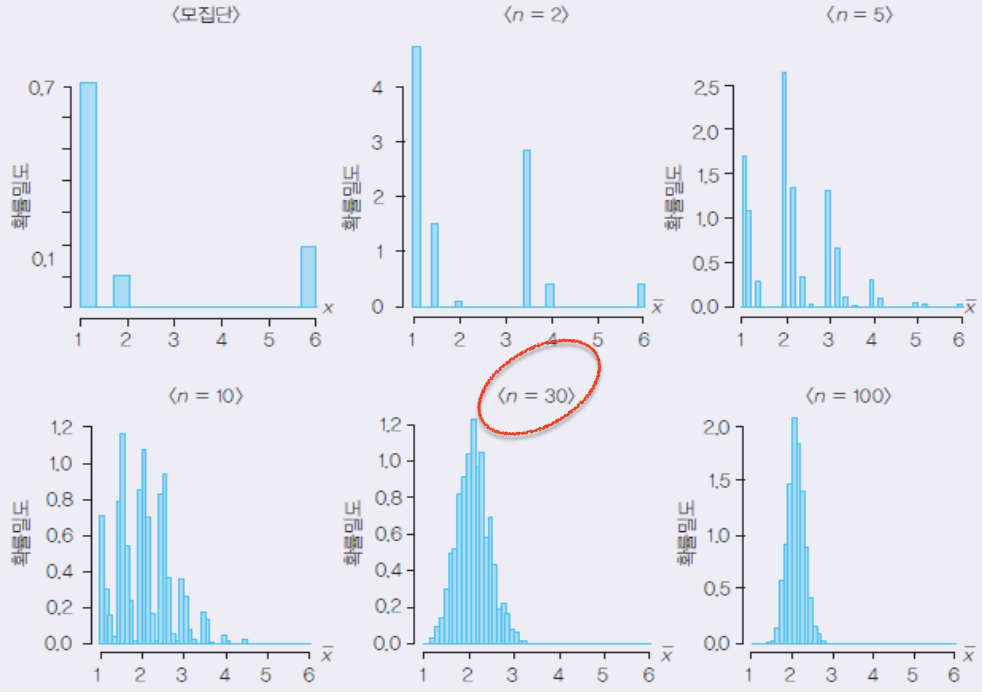
즉, n이 무한대만큼 커지면 추정량과 모수의 차이가 임의의 수 E보다 무조건 작아야 한다는 것이다.

-> X바, S^2, P^은 모두 불편성, 효율성, 일치성을 만족하므로 좋은 추정량이다.

6. 모평균 μ에 대한 구간추정

신뢰수준이 1 - α 로 정해지면 추정된 구간 [a, b]는 다음과 같은 특성을 갖는다.

P(a < θ < b) = 1 - α

이 때 추정된 구간 [a, b]를 신뢰구간이라고 한다.

* α : 오차율, 유의수준, 허용오차수준

< 신뢰구간의 일반화 >

점추정값 +- 오차한계

< 신뢰구간에 대한 해석 >

- 편의상 : 신뢰수준의 확률로 모평균이 신뢰구간에 있다.

- 정확한 : 다양한 표본평균에 따라 신뢰구간이 다양하게 나오는데, 이 중 모평균을 포함하는 신뢰구간의 비율이다.

< 모평균 μ에 대한 구간추정 공식 >

1) σ를 알기 때문에 σ를 사용하였고,Z분포를 사용할수있다.

2) σ를 모르기 때문에 S로 대신 사용하였고,

n이 30보다 클 때에는 Z분포를 사용할 수 있지만, 30보다 작으면 t분포만 사용할 수 있다.

7. t분포 구하기

X바 ~ (μ, σ^2/n)이면,

T = X바 - μ / (S / √n)~tn-1

(n-1은 자유도이다.)

t5%를 구하려면,

8. 모평균 μ의 신뢰구간 공식 정리

9. 모비율 p의 구간추정

- 모비율 p에 대한 100(1-α)% 신뢰구간(표본이 충분히 큰 경우)

1. 모수와 통계량의 관계 분석의 목적

-> 모수와 통계량의 관계를 찾으므로써 표본으로 모집단의 평균, 분산을 추론하기 위해 (추리 통계학)

1) 기술 통계학 : 주어진 자료의 특성을 분석한다.

2) 추리 통계학 : 자료가 추출된 모집단의 특성을 추론한다. 주어진 자료로부터 모집단의 평균, 분산을 추론한다.

2. 확률적 추출과 비확률적 추출

1) 전수조사 : 모집단 전체를 조사

2) 표본조사 : 모집단의 일부인 표본만을 대상으로 자료를 수집

-> 경제성, 자료수집 시간 단축, 정확성, 전수조사가 불가능할 때, 민감한 정보일 때

- 1 확률적 추출 : 개별 개체가 선택될 확률이 정해져 있는 경우 

ex) 단순무작위추출, 체계적 추출, 층화추출, 군집추출

- 2 비확률적 추출 : 개별 개체가 선택될 확률이 정해져 있지 않거나, 일부 개체가 선택될 가능성이 전혀 없는 경우

ex) 판단추출, 할당추출, 편의추출

3. 표본과 모수의 통계적 관계 : 평균과 분산

< 복원추출 가정 >

1) 표본평균들의 평균 = 모평균

2) 표본평균들의 분산 = 모분산 / n ( -> n은 추출한 개수 )

** 표본평균의 표준편차 보다는 표본평균의 표준오차 라고 부른다.

< 예시 >

모집단이 {10, 20, 30} 이고 n = 2, 복원추출한다고 가정하자

표본평균의 표본분포 )

표본평균들의 평균 = 10 x 1/9 + 15 x 2/9 + … + 30 x 1/9 = 20

표본평균들의 분산 = (10 - 20)^2 x 1/9 + (15 - 20)^2 x 2/9 + … + (30 - 20)^2 x 1/9 = 100/3 

모평균 = (10 + 20 + 30) / 3 = 20

모분산 = (10 - 20)^2 x 1/3 + (20 - 20)^2 x 1/3 + (30 - 20)^2 x 1/3 = 200/3

따라서, 모분산(200/3)을 n(2)로 나누면 표본평균들의 분산(100/3)의 관계가 있다.

모평균(20)은 표본평균들의 평균과(20) 동일하다.

3. 표본과 모수의 통계적 관계 : 표본추출오차

1) 표본추출오차 = 통계량 - 모수

통계량은 표본추출을 통해 추론한 모집단의 값이다.

예를 들어, 표본평균들의 평균으로 모평균을 추론할 때, 추론한 값(통계량)과 모평균의가 표본추출오차이다.

2) 평균의 경우

표본추출오차 = E[(표본평균의 평균 - 모평균)^2] 으로 구할 수 있다.

(+, - 를 상쇄를 방지하기 위해 제곱한다.)

E[(표본평균의 평균 - 모평균)^2]  = var(X바) = σ^2 / n

제곱근을 취하면, 

√E[(표본평균의 평균 - 모평균)^2] = σ / √n

즉, n이 커질수록, σ가 작을수록 표본추출오차가 작아진다.

3. 표본과 모수의 통계적 관계 : X바의 분포

1) X가 정규분포를 따를 때,

-> 모집단이 정규분포를 따르면, 표본평균은 표본크기와 상관없이 정규분포에 따른다.

2) X가 정규분포를 따르지 않을 때,

- 모집단의 크기는 일정하고, 표본의 크기가 다를 때,

- 표본의 크기는 일정하나, 모집단의 크기가 다를 때,

- > 모집단이 정규분포를 따르지 않을 때, 

모집단의 크기가 크고 표본크기가 크면 정규분포와 유사하다.

3) 중심극한정리

: 무한모집단에서 표본크기가 클수록 표본평균의 분포는 정규분포에 수렴한다.

ex) 

-> n이 30보다 크면 정규분포에 가깝다고 볼 수 있다.

정리하자면,

1) 모집단이 정규분포를 따르거나

2) 모집단이 정규분포를 따르지 않더라도, 모집단이 크고 표본크기가 30 이상이면

X바가 정규분포에 근사하다.

4. 표본평균의 구간확률 구하기

X바가 정규분포에 근사하면,

X바 ~ N(μ, σ / √n) 일 때,  Z = X바 - μ / (σ / √n) ~ N(0, 1) 을 활용한다.

5. 표본분산과 모수의 통계적 관계

모집단이 {10, 20, 30}으로 구성된다고 가정하자.

n = 2, 비복원 추출 가정

S^2 (표본분산)의 표본분포 )

E(S^2) = 0 x 3/9 + 50 x 4/9 + 200 x 2/9 = 600 / 9 = 200 / 3

즉, E(S^2) = σ^2 이다.

모집단이 정규분포를 따른다면, 카이제곱 분포를 활용할 수 있다. V = (n - 1) S^2 / σ^2 ~ X^n-1 

카이제곱분포는 비대칭 모양을 이루고, 오른쪽으로 긴 꼬리를 가지며 항상 양수값만을 갖는 특징이 있다.

카이제곱분포의 모양은 자유도에 따라 달라지는데, 이 자유도는 표본의 크기 n에서 1을 뺀 것과 같다.

자유도가 커질수록 카이제곱분포의 모양이 정규분포에 가까워진다.

6. 표본비율과 모수의 통계적 관계

ex) 모집단이 {R, B, B}로 구성되어 있다고 가정하자.

n=2, 복원추출을 가정한다.

p^(X/n)의 표본분포 )

E(P^) = 0 x 4/9 + 1/2 x 4/9 + 1 x 1/9 = 6/18 = 1/3

Var(P^) = (0-1/3)^2 x 4/9 + (1/2 - 1/3)^2 x 4/9 + (1-1/3)^2 x 1/9 = 1/9

즉,

E(P^) = p

Var(P^) = p(1-p)/n

E(X) = np

Var(X) = np(1-p)

으로 정리할 수 있다.